Over on the Berkeley SETI website, there's a section toward the bottom with some experiments to try:
- Reproduce the waterfall plot
- Determine the observed frequency (in GHz) of the coherent downlink carrier (main signal in the center of the waterfall plot), and the offset (in kHz) of the modulated subcarrier with the telemetry data
- Determine the drift rate of the above signals with time
- Calculate the Doppler velocity of Voyager with respect to Earth at the time of the observations
Radwave makes it possible to answer these questions without having to write any code or do any massive data downloads. Just download Radwave from the Google Play Store, tap the Menu button on the top left, then Public Collections, then the picture of Voyager 1. You can try figuring them out on your own (I love puzzles!) or keep reading to get some help. If you find any mistakes in my work, let me know @RadwaveRf on Twitter.
1. Reproduce the waterfall plot
A waterfall plot is another word for a spectrogram. The vertical natural of these plots, particularly when you've zoomed into time quite a bit and you're playing it in real-time, looks a bit like a waterfall. Radwave checks this box for you, time for experiment number 2.
2. Observed frequency and offset of subcarrier
First it might be helpful to watch https://www.youtube.com/watch?v=8ZJFzKcWejA&t=33s from 0:33 to 0:46. There we can see how to navigate to the Voyager 1 signal within the collection.
The picture below points out these different signal components. There are three different parts. The carrier is the spike in the middle, and the two smaller bumps on the right and left are the data portions.
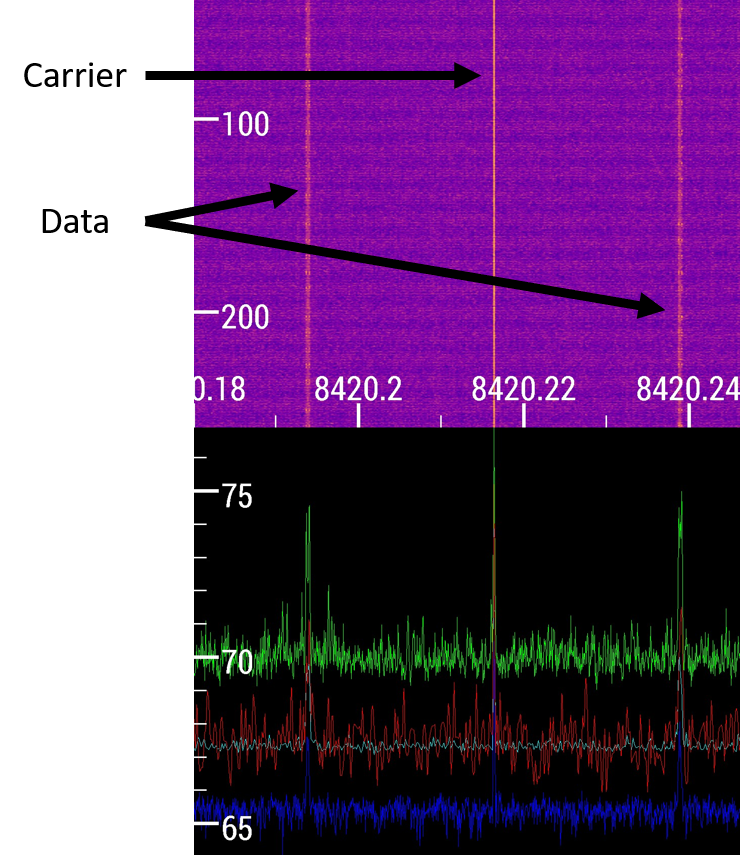
We can see that the carrier is located at about 8420.21642 MHz. Cool! There's our first answer!
The data subcarriers are at about 8420.1939 and 8240.23895 MHz. So to get the subcarrier offset, we just subtract these values from the carrier: 0.02252 MHz and 0.02253 MHz. To get that in kHz, we just multiply by 1000. So the subcarrier offset is about 22.5 kHz. Awesome! Two answers down. Next!
3. Calculate the drift rate
If we continue to zoom into these signals, we can see that they aren't completely vertical. They are a bit slanted.
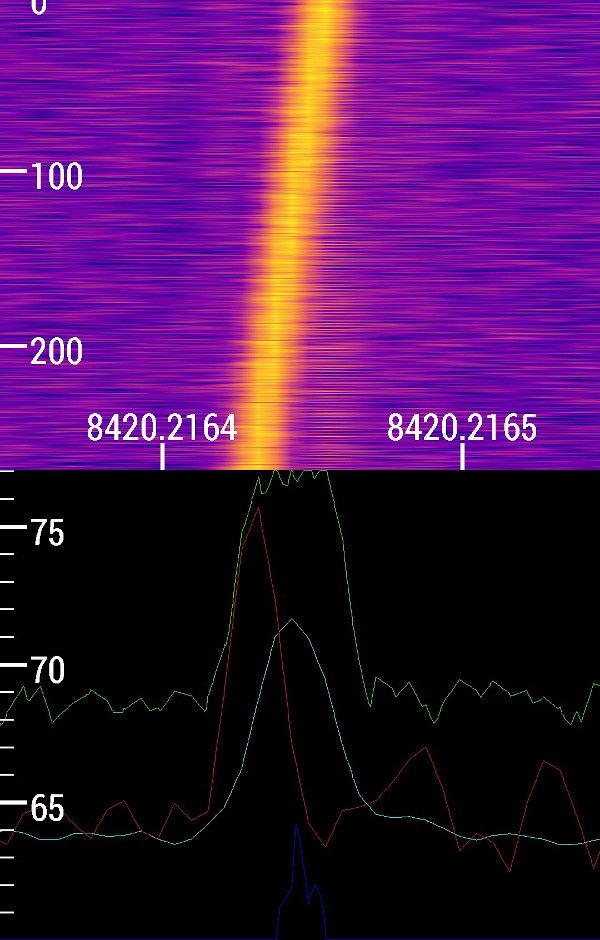
This is easiest to see in the carrier. The drift rate is the slope of the carrier line. The carrier starts at time 0 seconds at a frequency of about 8420.21645 MHz, and ends at a time of about 290 seconds at a frequency of about 8420.21625 MHz. To calculate the slope, we divide the difference of frequencies by difference of times: (8420.21625-8420.21645 MHz)/(290-0 seconds) = -0.69 Hz/second. That's three for three!
4. Calculate the Doppler velocity
Doppler is given by
fo = c/(c+v) * fe
where fo is the observed frequency, fe is the emitted frequency, c is the speed of light, and v is the Doppler velocity. We know the observed frequency from the spectrum, and we know the speed of light, but we don't yet know the emitted frequency. After a bit of googling, I found this paper on Voyager Telecommunications. Searching for "downlink carrier" (as taken from experiment 1 above) brings us to Table 2-1. That table says that the coherent downlink frequency for Voyager 1 is 8420.432097 MHz. That's pretty close to our observed frequencies, so that should be the right one. Solving for v above, we get
c+v = (c * fe)/fo
v = (c * fe)/fo - c
Substituting in our values, we get a Doppler velocity of +7677 meters/second. The plus means that Voyager 1 is moving away from Earth. That's pretty quick!
- Update March 26, 2024: Voyager Telecommunications
Bonus: Calculate the Doppler range
Let's assume that Voyager 1 is coasting through space, traveling at a constant velocity away from the sun. And we know that Earth is orbiting the sun at a known rate. So then we should be able to calculate the expected range of Doppler shifts for Voyager 1. This can help us know what range of frequencies to look for at any point in the year.
With some more googling, we can learn that the Earth is traveling at 107,000 km/hr = 29722 m/s as it goes around the sun. And Voyager 1 is traveling at 17000 m/s.
Since we're using a two body Doppler model, the equation changes slightly:
fo = (c-vo)/(c+ve) * fe
where ve is the emitter velocity (Voyager 1) and vo is the observer velocity (Earth). Depending on the time of year, Earth is traveling either toward or away from Voyager 1, so its minimum velocity is -29722 m/s and its maximum is 29722 m/s. Substituting everything in, we get a maximum observed frequency of 8420.806402 MHz and a minimum observed frequency of 8419.102511 MHz. So now you'll know where to look in the spectrum for Voyager all year long! You'll note that Earth actually moves faster than Voyager 1, so there are times of year when there is zero Doppler shift.

